به گزارش خبرگزاری خبرآنلاین و به نقل از زومیت، سال ۱۹۱۳، نامه‌ای عجیب به خانه‌ی یکی از برجسته‌ترین ریاضیدانان جهان در کمبریج انگلستان رسید. نویسنده‌ی نامه، جوانی هندی بود که می‌گفت فقیر است، هرگز به دانشگاه نرفته، اما فرمول‌هایی را کشف کرده که ادعا می‌کند پیام‌هایی از جانب خدایان هستند. این آغاز داستانی است که نه‌تنها دنیای ریاضیات را برای همیشه دگرگون کرد، بلکه یکی از غم‌انگیزترین روایت‌های تاریخ علم را رقم زد.

سرینیوآسا رامانوجان، نابغه‌ی خودآموخته‌ای بود که در فقر و بدون تحصیلات آکادمیک بزرگ شد و بخش عمده‌ای از پژوهش‌هایش را در انزوا در جنوب هند انجام داد. زمانی که ۲۴ ساله بود، شروع به ارسال مجموعه‌ای از نامه‌ها به ریاضی‌دانان برجسته کرد که اغلب نادیده‌ گرفته می‌شدند؛ تااینکه یکی از آن‌ها، جی. اچ. هاردی، متوجه شد که رامانوجان قادر است حقایق ریاضی را حس کند و به دنیاهایی دسترسی داشته باشد که دیگران به‌سادگی توانایی آن را نداشتند.

هاردی که خود دانشمند برجسته‌ای بود، به‌شوخی گفته بود بزرگترین خدمت او به ریاضیات، کشف رامانوجان بوده است. پیش از آنکه رامانوجان در سن ۳۲ سالگی از دنیا برود، هزاران نتیجه‌ی زیبا و شگفت‌انگیز از دنیای ریاضی ارائه کرد که اغلب بدون اثبات بودند و بیش از ۱۰۰ سال بعد، ریاضی‌دانان همچنان در تلاش‌اند تا خود را به نبوغ رامانوجان برسانند.

یعنی چه رازی در ذهن این نابغه نهفته بود که توانست بدون هیچ آموزش و ابزار مدرنی، حقایقی را ببیند که جهان علم تازه پس از یک قرن به درک آن‌ها رسیده است؟

نبوغی که در فقر شکوفا شد

سرینیوآسا رامانوجان در خانواده‌ای محترم اما فقیر در هند به دنیا آمد. آن‌ها به طبقه‌ی برهمن‌ها تعلق داشتند که بالاترین طبقه در سیستم طبقاتی هند محسوب می‌شود. در جامعه‌ی سنتی هند که ریشه در مذهب هندو دارد، مردم به پنج طبقه تقسیم می‌شوند و برهمن‌ها اغلب به‌عنوان معلم یا روحانی فعالیت می‌کنند. با اینکه تعلق به این طبقه معمولا به معنای ثروت بود، خانواده‌ی رامانوجان استثنا بودند و برای گذران زندگی، اغلب مجبور می‌شدند مستأجرانی را در خانه‌ی کوچکشان بپذیرند.

کانال Newsthink، رامانوجان را کودکی ساکت و متفکر توصیف می‌کند که از مدرسه بیزار بود. او در ابتدا چنان در برابر سیستم خشک آموزشی مقاومت می‌کرد که خانواده‌اش مجبور شدند برای بردن او به مدرسه، یک مأمور پلیس محلی را استخدام کنند. اما زمانی که خانواده در شهر کومباکونام ساکن شدند، نبوغ رامانوجان شروع به درخشیدن کرد. او نه‌تنها امتحانات را در نیمی از زمان مقرر تمام می‌کرد، بلکه معلمانش را نیز به چالش می‌کشید.

در یکی از کلاس‌ها، وقتی معلم توضیح می‌داد که هر عددی تقسیم بر خودش برابر با یک می‌شود، رامانوجانِ ۱۳ ساله پرسید: «اما آیا صفر تقسیم بر صفر هم یک می‌شود؟ اگر هیچ میوه‌ای را بین هیچ‌کس تقسیم کنیم، آیا باز هم هر کس یک میوه می‌گیرد؟» او حتی به مدرسه در تنظیم جدول زمانی پیچیده‌ی ۱۲۰۰ دانش‌آموز و ۳۶ معلم کمک می‌کرد؛ کاری که نیازمند محاسبات دقیق بود.

کتابی که زندگی‌اش را تغییر داد

در ۱۶ سالگی، اتفاقی افتاد که مسیر زندگی رامانوجان را برای همیشه عوض کرد. دوستی از کتابخانه کالج محلی، کتابی از جورج کار، ریاضیدان بریتانیایی به او داد که مجموعه‌ای از ۵۰۰۰ قضیه و فرمول ریاضی بود که پشت سر هم و تقریبا بدون هیچ توضیحی ردیف شده بودند؛ کتابی قدیمی که صرفا برای کمک به دانشجویان جهت حفظ کردن فرمول‌ها برای امتحانات نوشته شده بود.

برای اکثر دانش‌آموزان، خواندن چنین کتابی مانند کابوس بود، اما برای رامانوجان، این کتاب حکم جرقه‌ای در انبار باروت را داشت. رابرت کانیگل، زندگی‌نامه‌نویس رامانوجان، این کتاب را به «جدول کلمات متقاطعی با خانه‌های خالی» تشبیه می‌کند که التماس می‌کردند تا پر شوند. رامانوجان با شهود ذاتی خود، این خانه‌های خالی را پر کرد و با روش‌های منحصربه‌فرد خودش و دور از استانداردهای آکادمیک، شروع به کشف روابط بین اعداد کرد.

رامانوجان، پیوند عمیقی با مذهب داشت. او ریاضیات را یک مفهوم انسانی نمی‌دانست، بلکه آن را پنجره‌ای به ساختار جهان و افکار خداوند می‌دید. او بارها می‌گفت معادلات برای من هیچ معنایی ندارند، مگر اینکه فکری از جانب خداوند را بیان کنند. معروف است که او تمام کشفیاتش را مدیون الهامات الهه‌ی خانوادگی‌شان، «ناماگیری»، می‌دانست.

در خواب تجربه‌ای شگفت‌انگیز داشتم. پرده‌ای سرخ‌رنگ دیدم که گویی از خونِ جاری شکل گرفته بود. من نظاره‌گر آن بودم. ناگهان دستی پدیدار شد و شروع به نوشتن بر آن پرده کرد. سراپا محو تماشا شدم. آن دست، تعدادی انتگرال بیضوی نوشت. آن فرمول‌ها در ذهنم نقش بستند و به محض اینکه بیدار شدم، آن‌ها را روی کاغذ آوردم.

بروس برنت، ریاضیدان آمریکایی، در مصاحبه‌ای با فرانت‌لاین در سال ۲۰۱۳ گفته‌ بود: «بسیاری از مردم به‌اشتباه قدرت‌هایی ماورایی و عرفانی را به تفکرات ریاضی رامانوجان نسبت می‌دهند. اما این حقیقت ندارد. او با دقتی وسواس‌گونه، تک‌تک نتایج را در سه دفترچه‌ی خود ثبت کرده است.»

به گفته‌ی برنت، رامانوجان چنان وقت خود را صرف ریاضیات می‌کرد که حتی به معبد نمی‌رفت و همسر و مادرش اغلب غذا در دهان او می‌گذاشتند، زیرا فرصتی برای غذاخوردن نداشت. به گفته‌ی او، بیشتر داستان‌های مذهبیِ منتسب‌به رامانوجان، ساخته و پرداخته‌ی دیگران است. بااین حال، در پایبندی رامانوجان به احکام و آداب مذهبی، هیچ تردیدی وجود نداشت.

سقوط و تنهایی

باوجود نبوغ سرشار، زندگی آکادمیک رامانوجان خیلی زود به بن‌بست رسید. او چنان غرق در ریاضیات شد که از درس‌های دیگر غافل ماند. در کلاس‌های تاریخ روم، او مشغول نوشتن فرمول‌های دیفرانسیل و انتگرال بود. نتیجه این شد که بورسیه‌ی تحصیلی‌اش را از دست داد؛ فاجعه‌ای بزرگ برای خانواده‌ای که شهریه‌ی یک ترم دانشگاه، معادل یک ماه و نیم درآمد پدرشان بود.

فشار فقر و انتظارات خانواده باعث شد او از خانه فرار کند و حتی در کالجی دیگر ثبت‌نام کند، اما باز هم شکست خورد. در اوایل ۲۰ سالگی، او جوانی بیکار، بدون مدرک دانشگاهی و ناامید بود. رامانوجان تنها و منزوی، روزها در اسکله‌ی بندر مدرس (بندر چنای امروزی) به‌عنوان کارمند ساده کار می‌کرد و شب‌ها دفترچه‌هایش را با فرمول‌های جادویی پر می‌کرد. وقتی کاغذ کم می‌آورد، روی نوشته‌های قبلی با رنگی دیگر می‌نوشت. او می‌دانست این دفترچه‌ها تنها امید او برای نجات هستند.

نامه سرنوشت‌ساز به انگلستان

پس از اینکه ریاضیدانان محلی در هند نتوانستند عمق کار او را درک کنند، دوستانش او را تشویق کردند تا به غرب نامه بنویسد. سرانجام، او به گادفری هارولد هاردی، ریاضیدان برجسته در کالج ترینیتی کمبریج، نامه نوشت.

رامانوجان اثبات کرد جمعِ بی‌نهایت عدد مثبت برابر با کسری منفی می‌شود

هاردی و رامانوجان دو قطب مخالف هم بودند. هاردی یک آتئیست سرسخت، عاشق کریکت، متنفر از سیاستمداران و هواشناسی انگلستان بود که به منطق محض اعتقاد داشت؛ رامانوجان اما، مردی عمیقا مذهبی و متکی به شهود بود.

نامه‌ی رامانوجان در سال ۱۹۱۳ به دست هاردی رسید. جملات اول نامه، ساده و تکان‌دهنده بود: «من یک کارمند ساده در اداره‌ی بندر مدرس هستم…هیچ تحصیلات دانشگاهی ندارم…اما نتایجی به دست آورده‌ام که ریاضیدانان محلی آن را حیرت‌انگیز می‌خوانند.»

نامه‌ی ده صفحه‌ای رامانوجان پر از نتایج فنی بود؛ از فرمول‌هایی برای شمارش اعداد اول که کاری غیرقابل پیش‌بینی است تا قضایایی در مورد حساب انتگرال. اما ادعای «حیرت‌انگیز» او شامل مباحثی در مورد سری‌های واگرا بود؛ جایی که جمع تمام اعداد مثبت صحیح (۱، ۲، ۳ و…) تا بی‌نهایت، برابر با منفی یک‌دوازدهم می‌شد. ادعایی که در نگاه اول دیوانگی محض به نظر می‌رسید، اما بر پایه‌ی اصول پیشرفته‌ای از نظریه‌ی اعداد استوار بود.

چطور ممکن است جمعِ بی‌نهایت عدد مثبت، تبدیل به یک کسر منفی و کوچک شود؟ هاردی ابتدا فکر کرد این یک شوخی است، اما هرچه بیشتر به فرمول‌ها نگاه کرد، بیشتر حیرت‌زده شد. او با همکارش جان لیتل‌وود ساعت‌ها روی این فرمول‌ها کار کردند و درنهایت به این نتیجه رسیدند: «این فرمول‌ها باید درست باشند، زیرا اگر غلط بودند، هیچ‌کس آنقدر تخیل نداشت که چنین چیزهایی را اختراع کند.» آن‌ها فهمیدند که با یک نابغه طرف هستند.

ممکن است فکر کنید جمع رامانوجان بازی با اعداد است، اما نکته‌ی شگفت‌انگیز اینجاست که «منفی یک‌دوازدهم» در فیزیک کوانتوم واقعا کار می‌کند. مثلا نظریه ریسمان، برای اینکه از نظر ریاضی سازگار باشد، نیاز به ۲۶ بُعد دارد و محاسبات آن دقیقا به این نتیجه وابسته است. یا در اثر کازیمیر؛‌ انرژی بین دو صفحه فلزی در خلأ، با مجموع اعداد صحیح تا بی‌نهایت برابر است. اگر فیزیکدانان جواب را «بی‌نهایت» بگذارند، معادلات بهم می‌ریزد، اما اگر «منفی یک‌دوازدهم» بگذارند، نتیجه دقیقا با آزمایش‌های آزمایشگاهی مطابقت دارد.

سفر به سرزمین‌های ممنوعه

هاردی مصمم بود رامانوجان را به انگلستان بیاورد، اما یک مانع بزرگ مذهبی وجود داشت. طبق قوانین سخت‌گیرانه‌ی طبقه‌ی برهمن، سفر دریایی و عبور از آب‌های آزاد گناهی بزرگ محسوب می‌شد که می‌توانست باعث طرد شدن فرد از طبقه‌ی اجتماعی‌اش شود. مادر رامانوجان به شدت مخالف سفر رامانوجان بود.

اما یک رویا همه چیز را تغییر داد. مادر رامانوجان در خواب دید که پسرش در میان اروپایی‌ها نشسته و الهه ناماگیری به او دستور داد که مانع سرنوشت پسرش نشود. با این مجوز الهی، رامانوجان در سال ۱۹۱۴ سوار کشتی شد و به سمت انگلستان حرکت کرد. او لباس‌های غربی پوشید و موهایش را کوتاه کرد، اما نمی‌دانست که این سفر، قرار است برایش گران تمام شود.

زندگی در غربت و سرمای کمبریج

لندن و کمبریج برای رامانوجان دنیایی بیگانه بودند؛‌ شهرِ شلوغ، پر سروصدا و آب‌وهوایی که هیچ شباهتی به گرمای جنوب هند نداشت. به‌گفته‌ی کانال fern، او با آداب و رسوم غربی مشکل داشت؛ خوردن غذا با چاقو و چنگال برایش عذاب‌آور بود و آن را «فرو کردن فلز سخت در دهان» می‌دانست.

بااین حال، همکاری او با هاردی شکوفا شد. آن‌ها روزها روی دفترچه‌های رامانوجان کار می‌کردند. هاردی متوجه شد که رامانوجان به دلیل نداشتن آموزش رسمی، بسیاری از قضایای اثبات‌شده را دوباره کشف کرده است، اما بخش بزرگی از کار او کاملا جدید و انقلابی بود.

یکی از مشهورترین داستان‌های همکاری آن‌ها مربوط به زمانی است که هاردی با تاکسی شماره‌ی ۱۷۲۹ به دیدن رامانوجان رفت. هاردی گفت که این عدد خسته‌کننده و بی‌معنی است و امیدوار است برایش بدشانسی نیاورد، اما رامانوجان بلافاصله پاسخ داد:

«نه هاردی، این عدد بسیار جالبی است! ۱۷۲۹ کوچکترین عددی است که می‌توان آن را به دو روش مختلف به صورت مجموع مکعب دو عدد نوشت.»

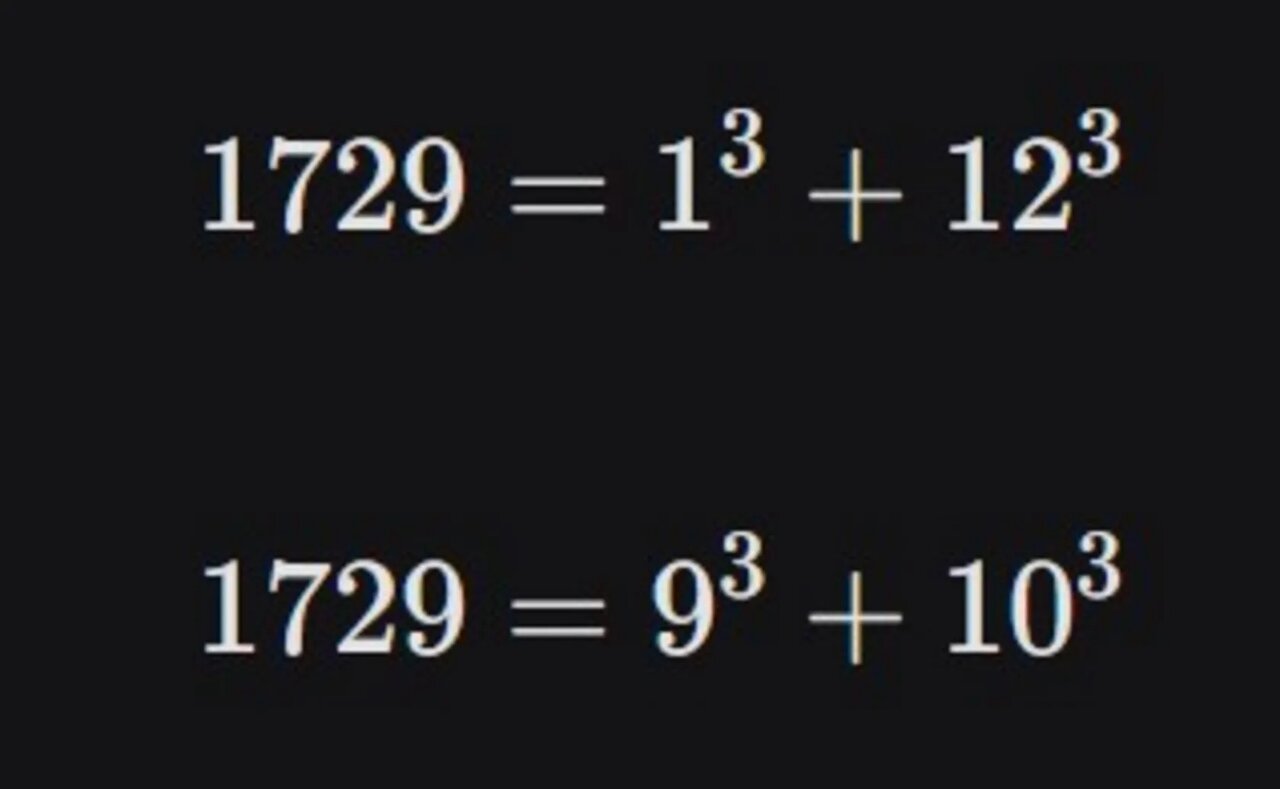
این عدد اکنون به عنوان «عدد تاکسی» شناخته می‌شود و رده‌ای از اعداد به نام «Taxicab numbers» را در ریاضیات ایجاد کرد.

مهم‌ترین دستاوردهای رامونجان

رامانوجان هزاران فرمول و رابطه‌ی ریاضی کشف کرد که بسیاری از آن‌ها سال‌ها جلوتر از زمان خودش بودند؛ اما شاید مشهورترین آن‌ها، افراز اعداد باشد؛ معادلاتی درباره‌ی روش‌های مختلفی که می‌توان یک عدد صحیح را به بخش‌های کوچکتر تقسیم کرد. این کار پایه‌گذار پیشرفت‌های بزرگی در فیزیک آماری و نظریه اعداد شد.

۱. افراز اعداد

از نظر بسیاری، افراز اعداد شاهکار بزرگ رامانوجان به‌شمار می‌رود. سوال ساده است: «به چند روش می‌توان یک عدد را با جمع کردن اعداد کوچک‌تر ساخت؟» مثلاً عدد ۴ را به ۵ روش می‌توان نوشت:

• ۱+۱+۱+۱
• ۱+۱+۲
• ۱+۳
• ۲+۲
• ۴

جواب این سوال برای اعداد کوچک، ساده است، اما برای اعداد بزرگ، تعداد روش‌ها به‌طرز وحشتناکی زیاد می‌شود. مثلا برای نوشتن عدد ۲۰۰، حدود ۴ تریلیون روش مختلف وجود دارد!

ریاضیدانان قرن‌ها دنبال فرمولی بودند که بدون شمردن تک‌تک حالت‌ها، بتواند تعداد این روش‌ها را پیش‌بینی کند. رامونجان با کمک هاردی فرمولی خیره‌کننده کشف کرد که با دقتی باورنکردنی تعداد این حالت‌ها را تخمین می‌زد. این کار مثل شمردن تعداد دقیق ستاره‌های یک کهکشان بدون تلسکوپ بود.

۲. فرمول‌های محاسبه عدد پی

رامونجان در سال ۱۹۱۴ مقاله‌ای منتشر کرد که شامل ۱۷ فرمول مختلف برای محاسبه عدد پی بود. ویژگی منحصربه‌فرد این فرمول‌ها «همگرایی بسیار سریع» آن‌هاست؛ یعنی با محاسبه تنها چند جمله اول، به تعداد زیادی رقم اعشار صحیح می‌رسید.

تا قبل از رامونجان، معروف‌ترین فرمول برای محاسبه پی معروف به فرمول لایب‌نیتس، آنقدر کند بود که برای به دست آوردن ۳۰۰ رقم اعشار، باید میلیاردها بار جمع و تفریق می‌کردید. اما با فرمول اول رامونجان، تنها با حدود ۳۵ بار محاسبه به همان دقت می‌رسید.

فرمول شاهکار زیر، امروزه اساس بسیاری از الگوریتم‌های کامپیوتری برای محاسبه میلیاردها رقم عدد پی است. ظاهرش ترسناک است، اما قدرتی باورنکردنی دارد:

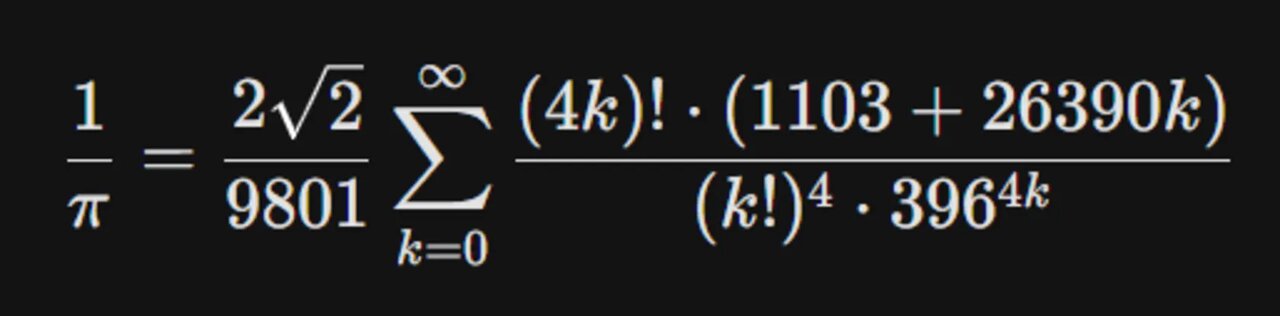
تنها با محاسبه‌ی اولین جمله‌ی این سری (یعنی k=۰)، به عدد پی تا ۸ رقم اعشار درست می‌رسید. هر جمله‌ی جدیدی که اضافه کنید، ۸ رقم اعشار دیگر به‌دقت اضافه می‌شود.

رامونجان علاوه‌بر سری‌های بی‌نهایت، فرمول‌های کوتاهی هم داشت که بدون نیاز به جمع‌بندی طولانی، تقریب بسیار دقیقی از پی می‌دادند. یکی از زیباترین آن‌ها، فرمول زیر است که عدد پی را تا ۶ رقم اعشار درست نشان می‌دهد:

۳. توابع ماک تتا

توابع ماک تتا (Mock Theta Functions) آخرین کشف رامونجان بود که آن را در بستر بیماری و تنها چند روز قبل از مرگش در نامه‌ای برای هاردی نوشت.

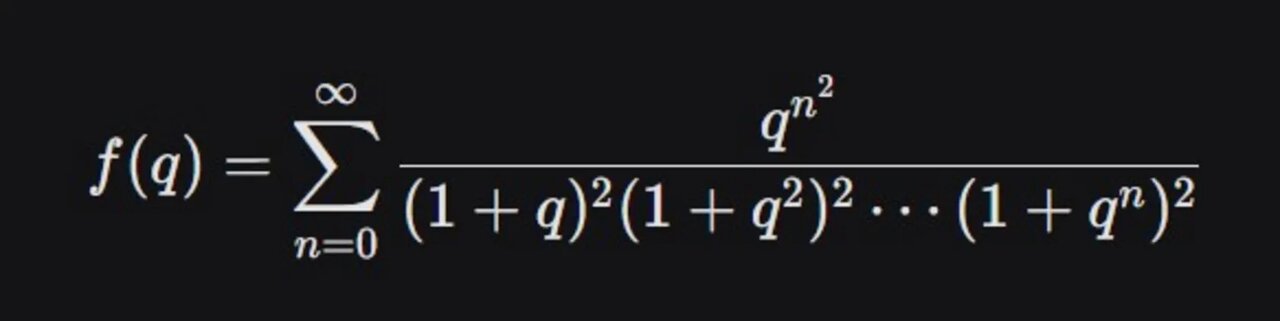
در آن زمان هیچ‌کس، حتی خود هاردی، دقیقا نفهمید این توابع چه کاربردی دارند و فقط معلوم بود که از نظر ریاضی درست هستند. حدود ۸۰ سال بعد، دانشمندان متوجه شدند که این توابع برای محاسبه‌ی آنتروپی سیاه‌چاله‌ها در نظریه ریسمان به آن نیاز دارند. انگار رامونجان یک قرن قبل، ابزار ریاضی مورد نیاز برای فیزیک کوانتوم آینده را پیش‌بینی کرده بود.

آغاز تراژدی؛ جنگ، گرسنگی و بیماری

همزمان با درخشش علمی رامانوجان، جنگ جهانی اول، اروپا را در تاریکی فرو برد. کمبود مواد غذایی شرایط را برای او که گیاهخوار سخت‌گیری بود، غیرقابل تحمل کرد. او اغلب فقط برنج و ماست می‌خورد و گاهی تنها با لیمو و نمک سر می‌کرد.

سرمای هوا نیز بلای جانش شده بود. در یک خاطره‌ی تلخ، دوستی او را در اتاقش دید که از سرما می‌لرزید و با پالتو خوابیده بود، درحالی که پتوها را مرتب و تاشده روی تخت گذاشته بود؛ چون رامانوجان نمی‌دانست که باید زیر پتو برود، نه اینکه آن‌ها را مثل روتختی استفاده کند.

کمبود تغذیه و استرس باعث شد او به بیماری سل یا مشکلات شدید گوارشی، مبتلا شود. او دو سال را در آسایشگاه‌ها و بیمارستان‌های مختلف گذراند. نامه‌های همسرش کمتر به دستش می‌رسید و احساس تنهایی و افسردگی او را احاطه کرده بود.

در اوج ناامیدی، رامانوجان در یکی از ایستگاه‌های متروی لندن خود را جلوی قطار انداخت. نگهبان توانست قطار را متوقف کند و او زنده ماند، اما دستگیر شد؛ چون خودکشی در آن زمان جرم بود. هاردی با نفوذ خود پلیس را قانع کرد که این مرد یک نابغه‌ی ملی است و نباید زندانی شود.

افتخارات و وداع

در سال ۱۹۱۸، درحالی که رامانوجان در بستر بیماری بود، خبر رسید که او به‌عنوان یکی از جوان‌ترین اعضای تاریخ «انجمن سلطنتی» (Royal Society) انتخاب شده است؛ یکی از بالاترین افتخارات علمی که نام‌هایی چون نیوتن و داروین را در خود داشت.

دلیل اصلی این انتخاب، فعالیتش روی «توابع بیضوی» (Elliptic functions) بود؛ توابعی که می‌توانند حرکات پیچیده، مانند حرکت سیارات به دور خورشید را که نه دایره‌ی کامل است و نه بیضی دقیق، توصیف کنند. این توابع مانند نقشه‌ای با جزئیات فوق‌العاده دقیق از رقص اجرام سماوی هستند.

کمی بعد، دانشگاه مدرس به او پیشنهاد حقوق سالانه داد و رامانوجان تصمیم گرفت به هند بازگردد، اما وقتی به هند رسید، مردی تکیده، رنگ‌پریده و افسرده بود. بااین‌حال، حتی در بستر مرگ، درحالی که از درد به خود می‌پیچید، دست از ریاضی نکشید. او در آخرین نامه‌ی خود به هاردی، درباره‌ی کشف جدیدش به نام «توابع ماک تتا» نوشت که دهه‌ها بعد توسط ریاضیدانان رمزگشایی شدند.

رامانوجان در ۲۶ آوریل ۱۹۲۰ و تنها در سن ۳۲ سالگی در کومباکونام از دنیا رفت؛‌ ریاضی‌دانان سراسر جهان او را نابغه‌ای شگفت‌انگیز می‌دانستند و اغلب جایگاهی هم‌تراز با بزرگانی همچون لئونارد اویلر و کارل ژاکوبی برایش قائل بودند.

رامانوجان از خود سه دفترچه یادداشت و دسته‌ای از اوراق که به «دفترچه گمشده» معروف است، به‌جا گذاشت؛ مجموعه‌ای حاوی بسیاری از نتایج منتشرنشده که ریاضی‌دانان تا سال‌ها پس از مرگش مشغول بررسی و اثبات آن‌ها بودند. زندگی و دستاوردهای علمی او در فیلم «مردی که بی‌نهایت را می‌شناخت» (۲۰۱۵)، به تصویر کشیده شده است.

هاردی سال‌ها بعد، کشف رامانوجان را بزرگ‌ترین دستاورد زندگی‌اش و «تنها حادثه‌ی عاشقانه» زندگی خود نامید. او در سخنرانی‌ای گفت: «من او را اختراع نکردم، او خودش را ساخت…اما من اولین فرد باصلاحیتی بودم که شانس دیدن کارهایش را داشتم و هنوز با رضایت به یاد می‌آورم که فورا تشخیص دادم چه گنجینه‌ای یافته‌ام.»

۵۸۳۲۳